Pour Some Syntactic Sugar on Me
El 31 de diciembre de 1984 fue una fecha que cambió para siempre la vida de Rick Allen, el baterista de Deff Leppard. En un accidente automovilístico, el “dios del trueno”, como le dicen sus fans, perdió su brazo izquierdo.
Para un joven y brillante baterista la amputación significaba el fin de su carrera, pero alentado por sus compañeros y con la ayuda de Jeff Rich (baterista de Status Quo), Allen trabajó en diseñar un kit electrónico, con este hizo su debut en 1986 en el festival Monstes of Rock en Castle Donington.
Rich usa cuatro pedales para su pie izquierdo, para reemplazar su miembro faltante, con los que gatilla el sonido del hit hat, bombo, caja y un tom.
Pero ocurrió que después del accidente de Allen la banda ingresó en su periodo más exitoso. Hysteria, el cuarto álbum de estudio de Deff Leppard fue el número uno en los rankings Billboard 200 y UK Album Charts de 1987. La historia está muy bien relatada en la película “Hysteria, the Def Leppard Story”.
La decisión de Rick Allen de usar la tecnología y modificar su forma de tocar la batería, para continuar con su carrera, es algo digno de estudiar en detalle. No todos nos enfrentamos a decisiones tan vitales como la que enfrentó este músico, pero en el mundo de la tecnología el cambio repentino es una constante.
Una lección del caso de Allen que podemos obtener es que la tecnología puede ser una gran ayuda para superar nuestras limitaciones físicas.

Rick Allen, baterista de Def Leppard
Kotlin
Los lenguajes de programación son una de las tecnologías que inventamos para superar la limitación que impone darle instrucciones a una Máquina de Turing. Lo que buscamos es poder expresarnos de la manera más cercana a como pensamos, y no de la forma secuencial que nos impone el modelo de Von Neumann, por ejemplo.
Es por esto que existen tantos lenguajes de programación, buscan superar alguna limitación.
Java es uno de los lenguajes más populares en este momentos, uno de los que tiene mayor penetración y representación en el mercado del desarrollo de software, de acuerdo a diversos índices, como el Ranking en RedMonk , o en Indice TIOBE.
Pero todos los que hemos programado en Java sabemos que no es un lenguaje cómodo, tiene alguna decisiones de diseño que aún generan grandes trastornos (como veremos en un ejemplo más adelante en este artículo).
La Java Virtual Machine fue creada para soportar el lenguaje Java, la idea de Gosling era portar esta máquina a diversos ambientes, principalmente dispositivos con limitados recursos. Pero Java está en casi todas partes, y distribuido masivamente en millones de dispositivos con Android.
Cuando Microsoft inventó .Net decidió tomar un camino inverso en cierta manera, al de Sun, su CLR es una máquina virtual pensada para trabajar con varios lenguajes, y cuando salió al mercado incluía a Visual Basic y C#.
Con el tiempo, la gente que usaba Java decidió construir otros lenguajes que aprovecharan la JVM, pero tratando de superar las limitaciones de Java.
Kotlin es uno de esos intentos. Un lenguaje que lleva ya seis años de desarrollo, y se encuentra en su versión 1.1.
No voy a escribir una elegía a Kotlin, Steve Yegge ya lo hizo en otro lado.
Es un lenguaje interesante, que hay que observar, creo que va a ganar tracción después del impulso que le dio oficialmente Google al reconocerlo como lenguaje oficial para Android.
Este artículo es una introducción al cuarto desafío de mi serie sobre estos “raros lenguajes nuevos”, así que vamos a eso, y después volvemos a Kotlin.
Syntactic Sugar
Pour your sugar on me
I can't get enough
– Def Leppard
Syntactic Sugar causes cancer of semicolons
– Alan Perlis
En los lenguajes de programación hablamos de Syntactic Sugar para referirnos a sintaxis diseñada para hacer las cosas más fáciles de leer, o de entender.
La idea del desafío cuatro es explorar esa Syntactic Sugar, junto con otras decisiones de diseño, que le dan alguna ventaja a cada uno de los lenguajes, y que explican porque hay tanta variedad de los mismos. También nos permite entender en qué estaban pensando sus autores cuando los crearon.
Esta vez, resolveré el problema un lenguaje a la vez y documentaré la solución por cada uno de los lenguajes en un post. Así que este cuarto desafío constará de nueve partes (o quizás 10 u 11).
El cuarto desafío
En esta oportunidad construiremos un programa que comprime información. Para esto usaremos un algoritmo clásico llamado Huffman Coding.
Al menos teóricamente, el Huffman Coding es la compresión que asegura que cada símbolo es represantado con la cantidad óptima de bits, de acuerdo a la teoría de la información de Shannon (de la que hemos hablado antes).
En el Huffman Encoding lo que hacemos es contar la frecuencia de los símbolos en el texto que queremos comprimir, en base a eso construimos una tabla de representación que minimice la cantidad de bits para cada uno. Así los símbolos más frecuentes requieren menos bits que los símbolos que se presentan menos veces en el texto.
Una descripción del código de Huffman más detallada está en Wikipedia, se las dejo para que la estudien si les interesa: Huffman Coding. Lo que importa ahora es cómo implementamos esto en diversos lenguajes. Así que iremos viendo esto a lo largo de los artículos.
Volvamos a Kotlin
Para construir una solución a este desafío necesitamos construir algunas estructuras de datos muy interesantes, como una Cola de Prioridad y un Trie. Esto último nos permite ver donde un lenguaje como Kotlin tiene ventajas sobre Java y nos ayuda a cometer menos errores, y escribir menos código.
Para explicarlo voy a tomar una desviación y les voy a proponer otro ejercicio. Supongamos que tenemos un árbol binario. En cada nodo de este árbol almacenamos un número, y queremos calcular la suma de estos números y los valores máximos y mínimos de este árbol.
Así, que nuestro objetivo es construir una estructura que cumpla lo siguiente:
Arbol es una estructura de arbol binario.
Un nodo tiene dos hijos siempre, y un valor numérico.
Una hoja sólo tiene un valor numérico.
Arbol.sum(): obtiene la suma de los valores en los nodos y las hojas.
Arbol.max(): obtiene el máximo valor entre los nodos y las hojas.
Arbol.min(): obtiene el mínimo valor entre los nodos y las hojas.
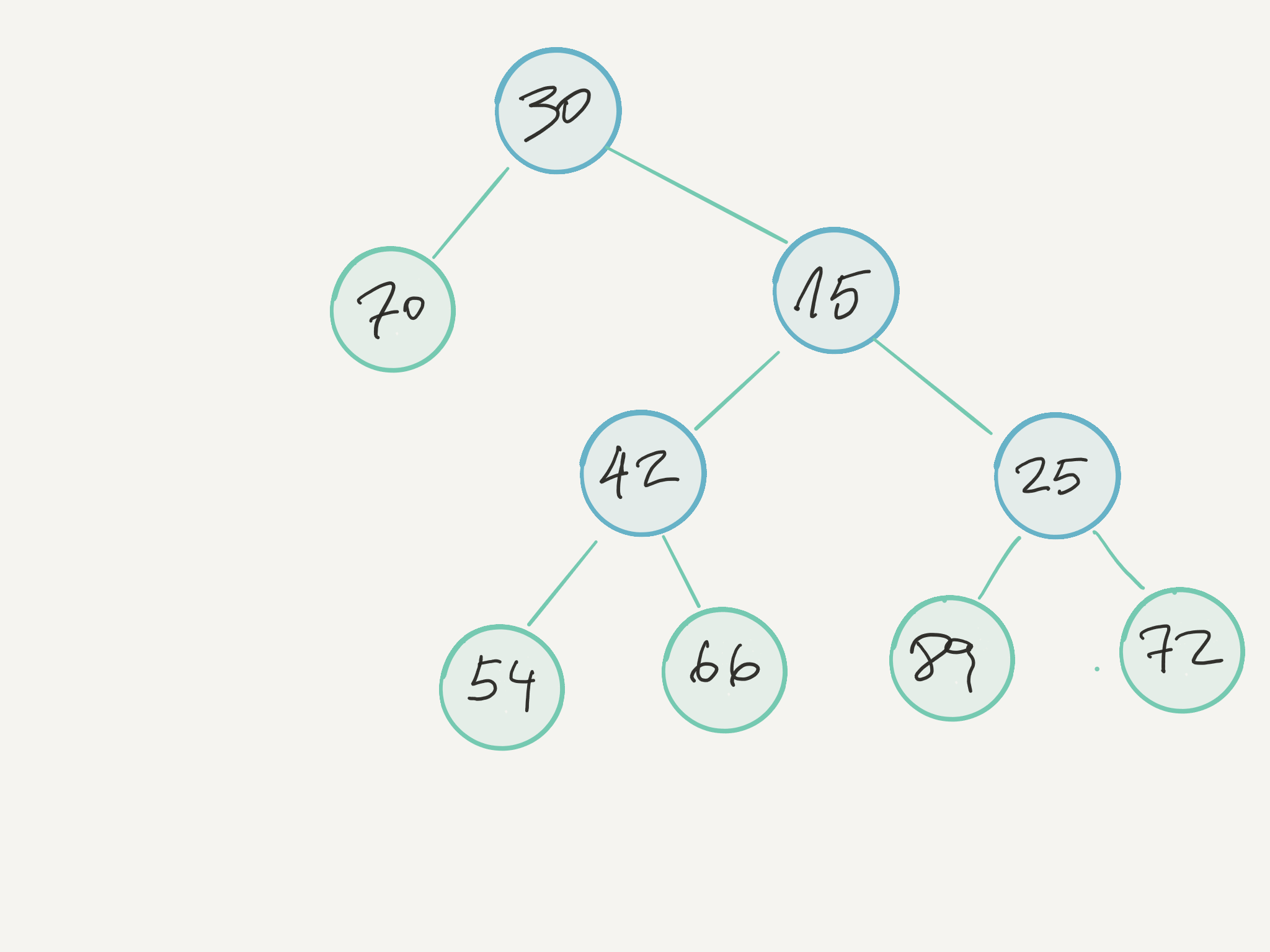
Un árbol binario con números en sus nodos y hojas
Una solución en Java es la siguiente:
public class Tree {
int value;
Tree left;
Tree right;
public Tree(int value) { this(value, null, null); }
public Tree(int value, Tree left, Tree right) {
this.value = value;
this.left = left;
this.right = right;
}
public int sum() {
return this.value + this.left.sum() + this.right.sum();
}
public int max() {
return Math.max(this.value, Math.max(this.left.max(), this.right.max()));
}
public int min() {
return Math.min(this.value, Math.min(this.left.min(), this.right.max()));
}
}
Y podemos crear el árbol de la figura de este modo:
Tree arbol = new Tree(30, new Tree(70), new Tree(15, new Tree(42, new Tree(54),
new Tree(66)), new Tree(25, new Tree(89), new Tree(72))));
System.out.println(arbol.sum()); // 463
System.out.println(arbol.max()); // 89
System.out.println(arbol.min()); // 15
Hay varios problemas con esta implementación, por ejemplo, ¿qué pasa con este código?:
Tree arbol = new Tree(30, new Tree(70), null);
Ups, una NPE! Entonces tenemos que parchar nuestro código de este modo:
public int sum() {
if (this.left == null && this.right == null) {
return this.value;
}
else if (this.left == null) {
return this.value + this.right.sum();
}
else {
return this.value + this.left.sum() + this.right.sum();
}
}
Y así para max y min, pero ¿estamos seguros de que ese código está bien?
Consideren esta solución en Kotlin:
interface Tree {
fun sum() : Int
fun min() : Int
fun max() : Int
}
class Node(val value:Int, val left:Tree, val right:Tree) : Tree {
override fun sum() : Int = value + left.sum() + right.sum()
override fun max() : Int = Math.max(value, Math.max(left.max(), right.max()))
override fun min() : Int = Math.min(value, Math.min(left.min(), right.min()))
}
class Leaf(val value:Int) : Tree {
override fun sum() : Int = value
override fun min() : Int = value
override fun max() : Int = value
}
Con esto podemos crear y usar nuestro arbol así:
val arbol = Node(30, Leaf(70),
Node(15, Node(42, Leaf(54), Leaf(66)), Node(25, Leaf(89), Leaf(72))))
println (arbol.sum())
println (arbol.max())
println (arbol.min())
No sólo el código es más compacto, sino que en Kotlin es imposible que podamos introducir un null en un árbol.
En Kotlin está prohibido tener variables sin inicializar por default.
Pero a veces es necesario introducir nulls en nuestras estructuras, y en ese caso, Kotlin introduce una Syntactic Salt, es decir, sintaxis que dificulta escribir cosas peligrosas, o malas prácticas.
Si quisieramos que nuestros nodos aceptara nulls entonces habría que declararlos así:
class Node(val value:Int, val left:Tree?, val right:Tree?) : Tree
Y tendríamos que manejar todas las condiciones de borde, ugh!
Así que Kotlin tiene esa ventaja incorporada y hay que aprovecharla.
Tony Hoare se lamenta de haber inventado Null al grado de llamarlo su error de “los mil millones de dólares”. Esta es una de las causas de mayores errores en nuestro código en Java. Kotlin en su modo normal impide eso, si quieres usar nulls debes tener bien claro qué estás haciendo y la sintaxis del lenguaje te lo indica en todo momento.
Un bug sutil
Pero hay una decisión de diseño en Kotlin que se refleja en un bug sutil, pero que me complicó cuando implementé la primera solución al desafío.
El bug se hace evidente en este código:
fun main(args:Array<String>) {
var list = ArrayList<Int>()
list.add(0)
list.add(0)
list.remove(list.size-1) o remove(int index)
list.forEachIndexed { i, v ->
println("list(" + i +") = "+v)
}
}
Uno esperaría que se imprimiera sólo uno elemento, pero se imprimen dos!
¿Por qué pasa esto?
Porque en Kotlin Int se traduce en el tipo Integer de Java, pero Java maneja eso como una clase distinta del tipo nativo int.
Por desgracia, la clase ArrayList tiene el método remove sobrecargado, del siguiente modo:
void remove(int index);
void remove(Object o);
Cuando pasas un Int en Kotlin el compilador utiliza la versión que recibe un objeto.
Así la llamada list.remove(list.size-1) se traduce como list.remove(new Integer(1)), como el número 1 no está en la lista tenemos que no se elimina nada de la lista, y no es la intención del programador.
La solución es usar el método removeAt(), pero en otras situaciones este bug se puede dar sin que nos demos cuenta. El compilador de Kotlin debería mejorar en este sentido con algún warning.
A diferencia de Scala, Kotlin construye sus colecciones ampliando las disponibles en Java. En Scala las colecciones son distintas, y existe un método de interoperar con Java algo más complicado, así que este sutil error no se da.
Huffman Coding en Kotlin
La ventaja de Kotlin en este ejercicio se muestra en la implementación del algoritmo de encoding.
En esencia el algoritmo para construir el árbol de codificación de Huffman es el siguiente:
Crear un nodo hoja para cada símbolo, asociando un peso según su frecuencia de aparición e insertarlo en la lista ordenada ascendentemente.
Mientras haya más de un nodo en la lista:
2.1. Eliminar los dos nodos con menor probabilidad de la lista.
2.2. Crear un nuevo nodo interno que enlace a los nodos anteriores, asignándole como peso la suma de los pesos de los nodos hijos.
2.3. Insertar el nuevo nodo en la lista, (en el lugar que le corresponda según el peso).
- El nodo que quede es el nodo raíz del árbol.
Para implementar esto en Kotlin, el árbol se representa así:
abstract class HuffTree(val frequency : Int)
class HuffLeaf(frequency: Int, val symbol: Char) : HuffTree(frequency) {
fun symbolIndex() : Int = ...
}
class HuffNode(val left: HuffTree, val right: HuffTree)
: HuffTree(left.frequency+right.frequency)
Y la construcción del árbol queda así:
fun buildTree(freqs : IntArray) : HuffTree {
// la lista ordenada la implementamos como un Heap
val heap = HuffHeap()
// Crea una hoja por cada símbolo con su frecuencia
freqs.forEachIndexed { sym, freq ->
if (freq > 0) {
heap.insert(HuffLeaf(freq, sym.toChar()))
}
}
// mientras haya más de un nodo en la lista
while (heap.size() > 1) {
val a = heap.extract()
val b = heap.extract()
heap.insert(HuffNode(a, b))
}
return heap.extract()
}
Si bien esto queda muy elegante, la implementación del Heap requiere que usemos un arreglo donde pueden haber nulls, y acá es donde aparecen las syntactic salt que mencionamos anteriormente:
class HuffHeap {
var heap = arrayOfNulls<HuffTree>(maxSymbols+1)
var last = 0
fun insert(tree:HuffTree) {
if (full()) {
throw ArrayIndexOutOfBoundsException()
}
last++
heap[last] = tree
var j = last
while (j > 1){
if (heap[j]!!.frequency < heap[j/2]!!.frequency) {
val tmp = heap[j]!!
heap[j] = heap[j / 2]!!
heap[j / 2] = tmp
}
j /= 2
}
}
....
al declarar heap como arrayOfNulls, obtenemos un arreglo de tipo Array<HuffTree?>.
Esto quiere decir que cada elemento del arreglo puede contener una referencia a un HuffTree y esta puede ser null.
De ahí que tengamos que hacer heap[j\]!!.frequency para acceder a la
frecuencia de un elemento del Heap.
Por construcción y si está bien implementado el TDA Heap, no hay modo de
que heap[j] sea null, así que la sintaxis !! nos dice que es seguro
usar ese valor y que no es un null.
Otra ventaja de Kotlin, y esto sí es un Syntactic Sugar, es que después de evaluar por un tipo podemos eliminar los engorrosos type casting de java, esto se ve en la función buildCodes()
fun buildCodes(tree : HuffTree, codes: Array<String>, prefix : StringBuffer) {
when (tree) {
is HuffLeaf -> codes[tree.symbolIndex()] = prefix.toString()
is HuffNode -> { ... }
}
}
Acá usamos la estructura de control when, que es una especia de switch, pero más poderoso, en este caso validamos el tipo de tree. Noten que si sabemos que tree es una HuffLeaf podemos invocar al método symbolIndex() que sólo existe en esa clase.
Esto ocurre en Swift, pero la verdad es que Swift parece haber tomado esta característica de Kotlin.
El código completo está en mi repositorio en GitHub. Hice dos implementaciones, una más orientada al objeto que la otra.
La diferencia del enfoque está expresada en estos dos fragmentos de código que implementan la misma función:
// función decompress versión 1
fun decompress(inputFile: String, outputFile: String) {
val input = BitInputStream(BufferedInputStream(FileInputStream(inputFile)))
val output = BitOutputStream(BufferedOutputStream(FileOutputStream(outputFile)))
val huffTree = readTree(input)
val length = input.readInt()
for (i in 0..length-1) {
var node = huffTree
while (node is HuffNode) {
val bit = input.readBoolean()
node = if (bit) node.right else node.left
}
if (node is HuffLeaf)
output.write(node.symbol)
}
output.close()
}
// función decompress versión 2
private fun decompress(inputFile: String, outputFile: String) {
val input = BitInputStream(BufferedInputStream(FileInputStream(inputFile)))
val output = BitOutputStream(BufferedOutputStream(FileOutputStream(outputFile)))
val huffTree = readTree(input)
val length = input.readInt()
(0..length-1).forEach { output.write(huffTree.readChar(input)) }
output.close()
}
En la versión 2 la case HuffTree se comporta cómo dicta el paradigma orientado al objeto y cada clase que la implementa sabe como comportarse según el contexto en que opera, esto es lo que se conoce como polimorfismo.
La gran diferencia es que HuffTree se declara de este modo:
abstract class HuffTree(val frequency : Int) {
abstract fun writeTo(output: BitOutputStream)
abstract fun dumpCodes(codes: Array<String>, prefix : StringBuffer)
abstract fun readChar(input: BitInputStream) : Char
}
Y para entender decompress hay que considerar que en HuffNode la función readChar se implementa así
// implementación en HuffNode
override fun readChar(input: BitInputStream) : Char {
val bit = input.readBoolean()
return if (bit) right.readChar(input) else left.readChar(input)
}
En cambio en HuffLeaf...
override fun readChar(input: BitInputStream) : Char {
return this.symbol
}
Todo esto para mostrarle que si bien Kotlin tiene el operador is, y when y que elimina cast, hay formas más adecuadas de desarrollar esto, o de lo contrario su código se transforma en una enorme secuencia de ifs o whens realizando type casting implícitos.
Conclusión
Kotlin es un lenguaje muy práctico, permite escribir código bastante compacto y expresivo. Muchas de sus construcciones además permiten escribir código más seguro. En Scala hay cosas similares, pero requieren más verbosidad (estoy pensando en los Options para evitar los nulls), pero esto es algo que vamos a discutir en el segudo artículo de esta serie.
Tiene estructuras que permiten ahorra typecasting y que permite ejecutar sentencias según el tipo de datos que ser recibe, pero esto puede llevar a malos hábitos de programación, siempre que sea posible usen el paradigma orientado a objetos adecuadamente, y eso pasa por usar polimorfismo.
Kotlin es un lenguaje moderno, entretenido, fácil de aprender, con la dosis adecuada de Sal y Azucar sintáctico se puede desarrollar casi cualquier cosa. Pero al igual que ocurre con la sal y azucar en nuestro alimentos, el abuso puede causar serios problemas de salud, así que úsenlo con moderación.
Todo el código que acompaña a este artículo se encuentra en Github: https://github.com/lnds/9d9l/tree/master/desafio4
Comentarios
comments powered by Disqus